LeetCode--判断矩形的两个角落是否可达
来记录一下最近写的LeetCode算法题,以免以后遗忘。“判断矩形的两个角落是否可达”是LeetCode上序号为3235的一道困难题,实现起来颇为复杂,现将整个思考解答过程记录如下:
题目
给你两个正整数 xCorner 和 yCorner 和一个二维整数数组 circles ,其中 circles[i] = [xi, yi, ri] 表示一个圆心在 (xi, yi) 半径为 ri 的圆。
坐标平面内有一个左下角在原点,右上角在 (xCorner, yCorner) 的矩形。你需要判断是否存在一条从左下角到右上角的路径满足:路径 完全 在矩形内部,不会 触碰或者经过 任何 圆的内部和边界,同时 只 在起点和终点接触到矩形。
如果存在这样的路径,请你返回 true ,否则返回 false 。
以下是官网给的示例,便于理解题目意思:
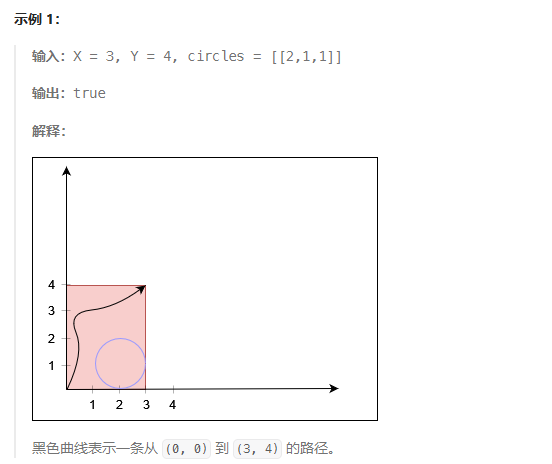
解题思路
分析题目,我认为可以从两个方面去考虑:
- 找到可以连接矩形两个角落的路径
- 证明所有的圆覆盖的区域完全阻塞了可能的路径
首先从第一个方向思考,要找到可以连接矩形两个角落的路径,可以从起点出发,不断探索可以延申的方向,通过深度搜索或者广度搜索,如果可以探索到一条到达右上角(目的角落)的路径,即说明存在这样的路径,如果遍历完全后,仍然没有可行解,则说明起点与终点之间被完全阻塞了。
考虑到在进行深度搜索或者广度搜索时,从一个节点出发的下一个节点的可能性是有限的,并且总的节点数目也应该是有限的,这样才能确保搜索到所有可能的路径。
但是题目中,并没有限制路径的经过节点,这条可能的路径将是可以任意曲折的,只要两点间存在区域没有被圆所覆盖,路径便可以经过。
此时我首先想从数学上找出一些限制条件,或者使得两点间可达的充分必要条件,考虑将整个矩形划分为网格,一个点所能达到的地方便是其四周八个点。但是在考虑的过程中,我发现无论怎样划分网格,下一个节点的可达性总是不一定影响再下一个节点的可达性。
此时选择从第二个方向思考,即考虑在怎样的情况下,所有可达的路径被圆覆盖。
由于最终所求的路径是从左下角到右上角,可以发现,只要从左边界或者上边界有一个连续的区域直达下边界或者右边界即可以确定不存在路径从左下角到右上角。如下图:

即只需确定一系列连续的圆从左边界或者上边界出发,可以从圆占据的区域内经过到达下边界或者右边界。这里考虑从左上边界出发(无论从哪边出发不影响结论)。而圆与圆间是否连续,可以通过两圆是否相交或者相切来判断。
此外,在编写代码之前,我们可以有以下条件:
- 任意一个圆,如果它与矩形区域没有任何重叠的地方,那么它不影响结论,可以去除
- 如果左上边界(或者右下边界)没有任何一个圆穿过它与矩形内部相交,那么一定存在紧贴与这个边界的路径连接矩形的两个角落。
- 如果两个圆虽然相交,但是相交的区域与矩形区域没有任何重叠,那么这种相交不能作为矩形内部圆连通的标志。
根据上述讨论,可以根据有效圆的相交相切关系,建立一棵表示连通关系的森林,森林中每一个节点即表示一个有效圆,每一条边表示一个有效连接关系。森林中每一棵树的根结点即为与左上边界相交或者相切的圆。注意:任何一个圆不可以既作为根结点又作为与根结点具有连通关系的子节点
之后根据广度搜索即可以探索出是否所有的路径都被阻塞。判断为被阻塞的终止条件是有节点与右下边界相交或者相切。
C++代码实现
class Solution
{
public:
bool canReachCorner(int xCorner, int yCorner, vector<vector<int>>& circles)
{
vector<vector<int>> path;
for(auto it=circles.begin();it!=circles.end();it++)
{
if (it->at(0) + it->at(2) <= 0 || it->at(0) - it->at(2) >= xCorner || it->at(1) + it->at(2) <= 0 || it->at(1) - it->at(2) >= yCorner)
{
circles.erase(it);
it--;
continue;
}
long long x1 = it->at(0), y1 = it->at(1), r1 = it->at(2);
if ((pow(x1, 2) + pow(y1, 2) <= pow(r1, 2)) || (pow(x1, 2) + pow(y1 - yCorner, 2) <= pow(r1, 2)) || (abs(x1) <= r1 && y1 >= 0 && y1 <= yCorner) || (abs(y1 - yCorner) <= r1 && x1 >= 0 && x1 <= xCorner) || ((x1 - xCorner)*(x1 - xCorner) + (y1 - yCorner)*(y1 - yCorner) - r1*r1 <= 0))
{
path.push_back(*it);
circles.erase(it);
it--;
}
}
if(!circles.size() && !path.size())
{
return true;
}
while (path.size())
{
vector<int> circle = path.front();
path.erase(path.begin());
long long x2 = circle[0], y2 = circle[1], r2 = circle[2];
if((x2*x2 + y2*y2 <= r2*r2) || ((x2 - xCorner)*(x2 - xCorner) + y2*y2 <= r2*r2) || ((x2 - xCorner)*(x2 - xCorner) + (y2 - yCorner)*(y2 - yCorner) <= r2*r2) || (abs(x2 - xCorner) <= r2 && y2 >= 0 && y2 <= yCorner) || (abs(y2) <= r2 && x2 >= 0 && x2 <= xCorner))
{
return false;
}
for (auto it=circles.begin();it!=circles.end();it++)
{
int x1 = it->at(0), y1 = it->at(1), r1 = it->at(2);
long long R = sqrt((x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2));
long long R_2 = (x1 - x2)*(x1 - x2) + (y1 - y2)*(y1 - y2);
if(R_2 <= (r1 + r2)*(r1 + r2))
{
double r1_2 = pow(r1, 2);
double r2_2 = pow(r2, 2);
double temp1 = (r1_2 - r2_2) / (2*R_2);
double temp2 = (sqrt(2*(r1_2 + r2_2) / R_2 - pow(r1_2 -r2_2, 2) / pow(R_2, 2) - 1)) / 2;
double a1 = (x1 + x2)/2 + temp1 * (x2 - x1);
double a2 = (y2 - y1) * temp2;
double b1 = (y1 + y2)/2 + temp1 * (y2 - y1);
double b2 = (x1 - x2) * temp2;
if ((a1 + a2 < 0 && b1 + b2 < 0 && a1 - a2 < 0 && b1 - b2 < 0) || (a1 + a2 > xCorner && b1 + b2 > yCorner && a1 - a2 > xCorner && b1 - b2 > yCorner))
{
continue;
}
path.push_back(*it);
circles.erase(it);
it--;
}
}
}
return true;
}
};