问题描述

给你一个整数 n 和一个二维整数数组 queries。有 n 个城市，编号从 0 到 n - 1。初始时，每个城市 i 都有一条单向道路通往城市 i + 1（ 0 <= i < n - 1）。 queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向道路。每次查询后，你需要找到从城市 0 到城市 n - 1 的最短路径的长度。返回一个数组 answer，对于范围 [0, queries.length - 1] 中的每个 i，answer[i] 是处理完前 i + 1 个查询后，从城市 0 到城市 n - 1 的最短路径的长度。

有如下示例：

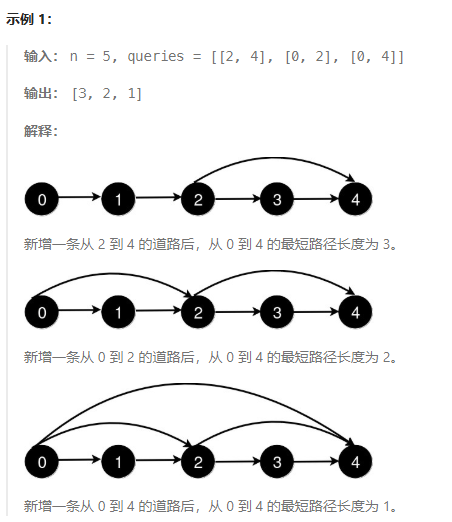
alt text

分析

面对此题，第一时间考虑的是广度优先搜索，一层一层遍历每一种可能的路径，考虑到每一条路径的权重都是1，最先达到终点的即为最短路径。此外，考虑到最终的最短路径中，考虑到达终点的前一个节点，从起点到该节点的路径也必须是最短路径，据此可递推得到最终的最短路径，且考虑到在每一次添加数组queries中的边时，只有queries[i][1]及其之后的节点可能被影响，故在每次查询时，也只需重新计算从queries[i][1]之后的节点最短路径。

但是考虑到该题为最短路径问题，可以使用Dijkstra算法在每一次查询时计算最短路径。此解法并非最优，但这里用这种算法主要用于记录一种DIjkstra算法的C++的实现方式。

代码

#include <vector>
#include <queue>
#include <limits>
using namespace std;

struct Edge
{
    int to;
    int weight;
    Edge() = delete;
    Edge(int to, int weight): to(to), weight(weight){}
};
using Graph = vector<vector<Edge>>;


class Solution 
{
private:
    

public:
    vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) 
    {
        Graph graph;
        vector<int> answer;
        int q_num = queries.size();
        graph.resize(n);
        for (int i = 0; i < n-1; i++)
        {
            graph[i].emplace_back(i+1, 1);
        }
        for (int i = 0; i < q_num; i++)
        {
            graph[queries[i][0]].emplace_back(queries[i][1], 1);
            int ans = Dijkstra(graph, 0);
            answer.emplace_back(ans);
        }
        return answer;
    }

    int Dijkstra(const Graph& graph, int start)
    {
        int n = graph.size();
        vector<int> dist(n, __INT_MAX__);
        dist[start] = 0;

        // <distance, destination>
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
        pq.emplace(0, start);

        while (!pq.empty())
        {
            auto [curr_dist, curr_vertex] = pq.top();
            pq.pop();

            if(curr_dist > dist[curr_vertex]) continue;

            for(const Edge& edge:graph[curr_vertex])
            {
                int new_dist = edge.weight + curr_dist;
                if(new_dist < dist[edge.to])
                {
                    dist[edge.to] = new_dist;
                    pq.emplace(new_dist, edge.to);
                }
            }
        }

        return dist.back();
        
    }
};

这里记录图的结构体、选取最小距离时所用到的优先队列是之前不熟悉的用法，故记录在此。