问题描述

给你一个整数 n 和一个二维整数数组 queries。

有 n 个城市，编号从 0 到 n - 1。初始时，每个城市 i 都有一条单向道路通往城市 i + 1（ 0 <= i < n - 1）。

queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向道路。每次查询后，你需要找到从城市 0 到城市 n - 1 的最短路径的长度。

所有查询中不会存在两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。

返回一个数组 answer，对于范围 [0, queries.length - 1] 中的每个 i，answer[i] 是处理完前 i + 1 个查询后，从城市 0 到城市 n - 1 的最短路径的长度。

以下为题目的一个示例：

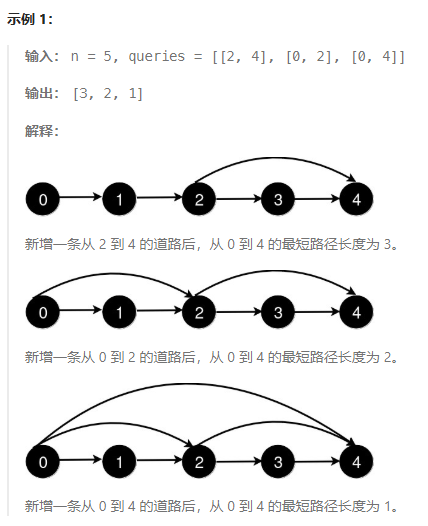
alt text

分析

面对此题时，我首先尝试了在新增道路查询后的最短距离1中所用到的Dijkstra算法，但是在第638个测试用例中，显示超时。

接下来考虑动态规划算法，考虑到在这道题中，所有查询中不会存在两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]，故任一节点的最短距离取决于它前一个节点的最短路径，考虑使用两个数组，一个记录每个节点的最短距离，一个记录每个节点在计算得到的最短距离中其前一个节点。

在经过依次查询后，重新计算query[1]及其之后的最短距离并更新前驱节点。此外，考虑到若在之后某一节点其前驱节点在query[0]及之前，则该节点及之后的节点的最短距离和前驱节点都不会被本次查询所影响。

动态规划代码

#include <vector>
using namespace std;

class Solution
{
public:
    vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) 
    {
        vector<int> dist(n);
        vector<int> prev(n);
        for (int i = 0; i < n; i++)
        {
            dist[i] = i;
            prev[i] = i-1;
        }
        prev[0] = 0;

        vector<int> answer;
        for (auto &query:queries)
        {
            
            if (dist[query[0]] + 1 < dist[query[1]])
            {
                int value = dist[query[1]] - (dist[query[0]] + 1);
                dist[query[1]] = dist[query[0]] + 1;
                prev[query[1]] = query[0];
                for (int i = query[1] + 1; i < n; i++)
                {
                    if (prev[i] <= prev[query[1]])
                    {
                        break;
                    }
                    dist[i] = dist[i] - value;
                    
                }
                
            }
            answer.emplace_back(dist.back());
        }
        return answer;

    }
};

删除算法

但是在提交之后，发现在638个用例仍然未能通过，问题为时间超出限制。重新考虑该问题，可以发现每一次查询后所添加的边所跨越的节点对之后所有节点的计算都不影响，如果删除这些被跨越的节点，那么每一次查询后到终点的最短距离就是总节点集合的大小。

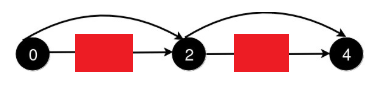
alt text

重新编写代码，使用set记录总节点，每次查询时，删除在查询范围内的节点，添加当前集合的大小，代码记录如下：

#include <vector>
#include <algorithm>
#include <set>
#include <numeric>
using namespace std;


class Solution
{
public:
    vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) 
    {
        vector<int> dist(n);
        iota(dist.begin(), dist.end(), 0);
        set<int> curr(dist.begin(), dist.end());

        vector<int> answer;
        for (auto &query:queries)
        {
            auto start = curr.lower_bound(query[0] + 1);
            auto end = curr.upper_bound(query[1] - 1);
            curr.erase(start, end);
            answer.emplace_back(curr.size()-1);
        }
        return answer;

    }
};