数学建模 网络最大流
网络最大流都是建立在流网络上的,流网络可以被表示为一个有向图
并且在这个有向图中,每条边同时有两个属性:
- 当前边的最大容量
- 当前边的已使用容量
同时对于图中的每一个节点,所有流入当前节点的容量等于所有流出该节点的容量
下边是一个流网络的示例:
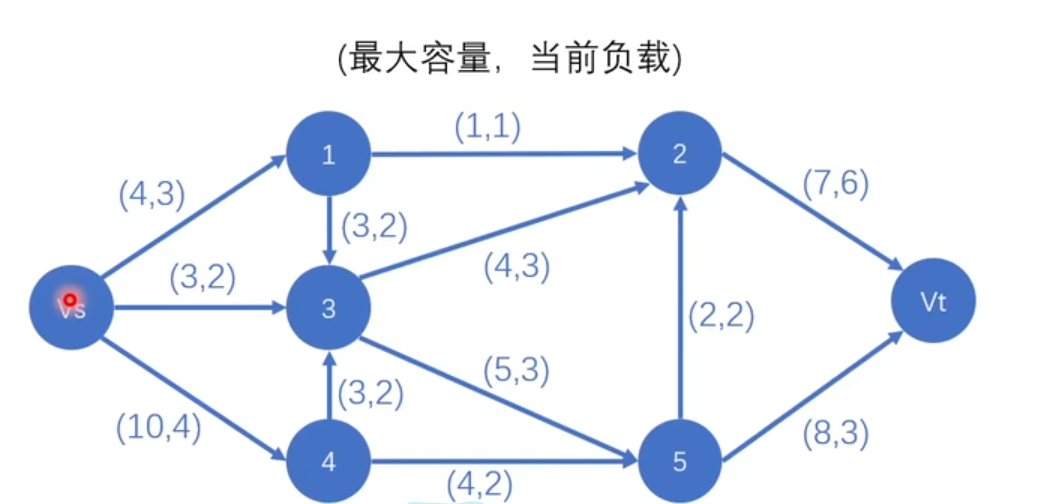
求解网络最大流问题就是求解网络的一种状态,使得源节点到目标节点的流量最大。
求解方法
要求解这个问题只须依次找到该网络的所有增广路,并通过合适的方式消除增广路即可。 增广路指的是网络中一条从源节点到目标节点的路径,在该路径上增加流量而不会使得某一条边的负载超出其最大负载。
在Ford Fulkerson求解算法中 对于除源节点以外的任意一个节点$V_j$用标号$(+V_{i}, \Delta_{j})$,其中用‘+’表示前向弧,‘-’表示反向弧,$\Delta_{j}$表示改变量。其中,源节点用$(0, \inf)$,即假定从源节点有源源不断的输入。
- 从源节点出发,依次寻找源节点可以抵达的下一个节点,如果存在可用的容量,延伸到下一个节点,其中$\Delta_{j}$使用上一个节点与延伸节点中较小的值
- 重复进行直到延伸到目标节点,其中,在下方的例子中,通过该增广链可增加的量为$min(\inf, 1, 1, 1) = 1$。最终使得该增广链上的每一条弧都+1。
- 重复进行直到网络中没有增广路,即为最终的最大流。
